Assessing the absolute neutrino mass scale is one of the major challenges in today particle physics and astrophysics. This requires to measure the mass of one of the three neutrinos and the kinematical neutrino mass measurement is the only model independent method since it exploits only energy and momentum conservation. In particular, the electron anti-neutrino mass can be measured by precisely analyzing the kinematics of electrons emitted in beta decays. In practice this means measuring the minimum energy carried away by the anti-neutrino, i.e. its rest mass, by observing the highest energy electrons emitted in the decay.
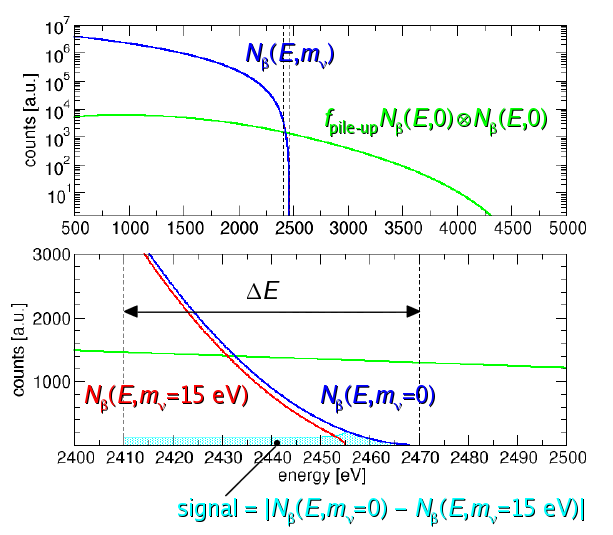 |
| Top: Calorimetric energy spectrum of 187Re decay compared with the pile-up spectrum. Bottom: Zoom around the end point, with a comparison between 0 and finite-neutrino-mass beta spectra |
For years, laboratory experiments based on the study of proper nuclear processes have been used to directly measure the neutrino masses. In particular, single beta decay has been, historically, the traditional and most direct method to investigate the electron (anti)neutrino mass. In fact, this kinematical direct measurement exploits only energy and momentum conservation and therefore it is the only one which permits to estimate neutrino masses without theoretical assumptions on neutrino properties and in a completely model-independent way.
Direct kinematical neutrino mass experiments, which study nuclear beta decays, look for a deformation in the energy spectrum of visible particles – i.e. electrons - in an interval ∆E where neutrino kinetic energies approach zero - i.e. at the spectrum end-point Q. The fraction of these events in beta decay is only proportional to (∆E/Q)3 and low Q beta decays are therefore used, like 3H (Q≈18keV) or 187Re (Q≈2.5keV).
To date, the study of the beta decay of
tritium (3H) using
electrostatic β-spectrometers has been the most sensitive approach, yielding an upper limit on the electron anti-neutrino mass of 2.2 eV (
Mainz experiment). In the near future, the
KATRIN experiment will analyze the 3H beta decay end-point using the most intense
3H source ever built and a 1 eV resolution electrostatic spectrometer: the expected statistical sensitivity is about 0.2 eV.
However, these spectrometric experiments suffer from many systematic uncertainties because the measured electron energy has to be corrected for the energy lost in exciting atomic and molecular states, in crossing the source, in scattering through the spectrometer, and more. Calorimetric measurements in which the beta source is embedded in the detector are an appealing alternative to spectrometry. In this configuration the energy emitted in the decay is entirely measured by the detector, except the fraction taken away by the neutrino. This eliminates the systematic uncertainties arising from an external electron source and in principle can be applied also to a variety of beta decaying isotopes.
A perfect practical way to make a calorimetric measurement is to use
low temperature microcalorimeters, where all excitations from an interaction are allowed to decay to near thermal equilibrium thus producing a temperature rise of the detector that can be measured by a sensitive thermometer to determine the deposited energy. The measurement is then free from the systematic effects induced by possible energy loss in the source and it is not affected by uncertainties related to decays on excited final states. If no meta-stable states exist in the material all the decay energy is integrated and collected in a short time regardless of its origin: X-ray, auger electron or recoil. Since calorimeters detect all the decays occurring, the source activity must be limited to avoid spectral distortions and background at the end-point due to pulse pile-up. The consequent limitation to the statistics can be balanced by using beta decays with a low end-point energy
Q, like that of
187Re
Several investigations have been carried out on microcalorimeters for a calorimetric neutrino mass measurement with 187Re as probe isotope. Because of 187Re isotopic natural abundance of about 63%, a metallic Rhenium crystal can be used as detector absorber for calorimetry. Rhenium metal undergoes a normal to superconducting transition at Tc = 1.7 K, so that the electronic specific heat vanishes at the very low T/Tc at which it is operated. This has allowed the use of a relatively large amount of Rhenium metal (about 1000 mg). However metallic Rhenium exhibits two major difficulties: the low specific activity of about 1 Bq/mg and the relative slowness of the thermalization process. Also dielectric compounds in proper crystalline forms can be used, but they do not completely circumvent the metal problems, since they have even lower specific activities and they face an incomplete thermalization of the deposited energy.
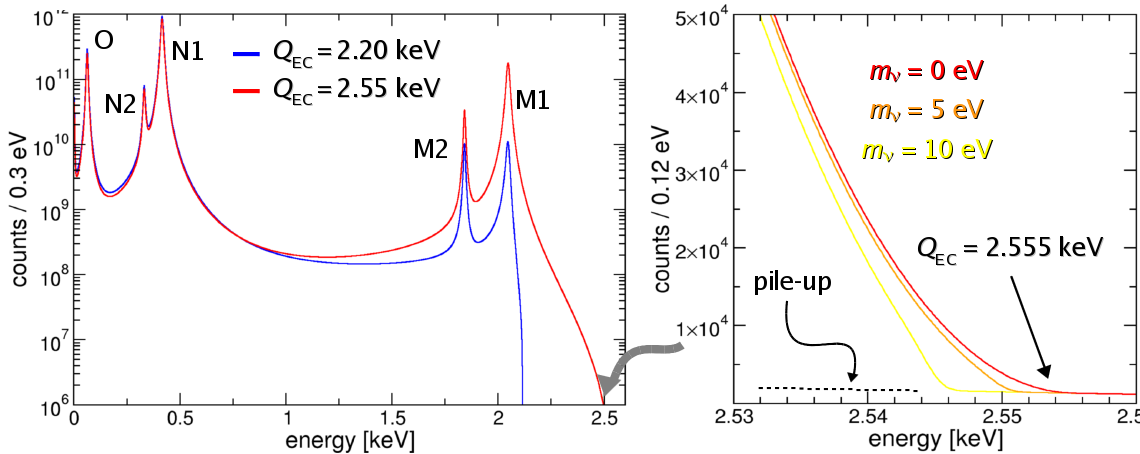
It was suggested thirty years ago that electron capture (EC) decays with low Q-values could be used as an alternative to single beta decay for the direct determination of the electron neutrino mass.163Ho decays by EC to 163Dy with a half life of about 4570 years and with the lowest known Q-value (about 2.6 keV), which allows captures only from the M shell or higher.
In a calorimetric EC experiment the same neutrino phase space factor [(Q-Ee)2- mν2]1/2 appears as in a beta decay spectrum, with the total de-excitation energy Ec replacing the energy of the electron Ee. The de-excitation energy Ec is the energy released by all the atomic radiation emitted in the process of filling the hole left by the EC process, mostly electrons with energies up to about 2 keV (the fluorescence yield is less than 10-3). The calorimetric spectrum appears as a series of lines at the ionization energies Ei of the captured electrons. These lines have a natural width of a few eV and therefore the actual spectrum is a continuum with marked peaks with Breit-Wigner shapes.
 |
|
Left: Calorimetric energy spectrum of 163Ho EC decay calculated for ∆E=2eV andfpp=10-6 and for two Q-values. Right: Blow up of the spectrum in the vicinity of the end-point.
|
- SNOWMASS 2021 "Prospects for neutrino mass in other isotopes": slides

